Why Specified Complexity is Key to Detecting Design

In plain English what specified complexity is and why it is able to detect design

The General Problem

I recently wrote a paper titled “Specified Complexity Made Simple,” which appeared on my blog and was reprinted at Evolution News. It explains specified complexity for non-technical readers. It lays out what specified complexity is and how it is used to detect design. But that paper doesn’t explain why specified complexity works—why it is precisely what’s needed to detect design. That’s the task of this paper.

What, then, is specified complexity and why is it able to detect design? To answer this question, I’m going to proceed from first principles. Thus, rather than rehearse the technical details underlying specified complexity and the mechanics of using it, I want here to lay out the problem that led to the formulation of specified complexity in the first place and show why specified complexity is what’s needed to resolve it.

The problem that specified complexity is intended to resolve is this: given some event (or object or structure produced by an event) for which we don’t know exactly how it came about, what features of it could lead us rightly to think that it was the product of an intelligent cause? This question asks us to engage in effect-to-cause reasoning. In other words, we see an effect and then we must try to determine what type of cause produced it.

The problem that specified complexity attempts to resolve therefore differs from detecting design through cause-to-effect reasoning. In cause-to-effect reasoning, we witness a known cause and then track its effect. Thus we may see someone take hammer and chisel to a piece of rock and then watch as an arrowhead is produced. Detecting design in such a case is obvious because we know that the person shaping the rock is an intelligent agent, and we see this agent in real time bring about an artifact, in this case an arrowhead.

With specified complexity, however, we are not handed a smoking gun in the form of an intelligent agent who is clearly witnessed to produce a designed object. Rather, we are simply given something whose design stands in question (such as a chunk of rock), and then asked whether this rock has features that could reasonably lead us to think that it was the product of design (such as the rock taking the shape of an arrowhead).

So, the question specified complexity raises can be reframed as follows: Given an event whose precise causal story is unclear, what about it would convincingly lead us to conclude that it is the product of intelligence? For simplicity, we’ll focus on events, thereby tacitly identifying physical or digital items with the events that produce them. To further simplify things, let’s look at one type of example that captures what’s at stake in this question.

SETI and the Shannon Communication Diagram

Consider, therefore, the case of SETI, or the search for extra-terrestrial intelligence. SETI researchers find themselves at the receiving end of the classic Shannon communication diagram:

This diagram, which figures centrally into Claude Shannon’s 1949 book The Mathematical Theory of Communication, tracks information from a source to a receiver in the presence of noise. In formulating this diagram, Shannon assumed that the information source was an intelligent agent. But that’s not strictly speaking necessary. It could be that the source of the signal is unintelligent, such as a stochastic or deterministic process. Thus a quantum device generating random digits may be at the source.

Receiving signals at the far end of this diagram, SETI researchers want to know the type of cause responsible for the signals at the other end. To keep things simple, yet without loss of generality, let’s assume that all the signals that the SETI researchers receive are bitstrings, that is, sequences of 0s and 1s. There’s a lot of radio noise coming in from outer space. There are also a lot of humanly generated radio signals the SETI researchers will need to exclude. So, given a radio signal in the form of a bitstring that’s verifiably from outer space—and thus not humanly generated—how can we tell whether it is the product of intelligence?

Notice that the problem here is not as in the film ET, where an embodied alien intelligence actually lands on Earth and makes itself immediately evident. Rather, as in the film Contact (based on a novel of the same name by Carl Sagan), all the SETI researchers have to go on is a signal, and the question is whether its source is intelligent or non-intelligent. Any such intelligence is not immediately evident. Rather, such an intelligence is mediately evident. In other words, the intelligence is mediated through the signal, the medium of communication.

The problem confronting the SETI researchers bears an interesting resemblance to the Turing test. In the Turing test, a human must determine whether the source of a message is a computer or a human. If a computer can behave indistinguishably from a human, then the Turing test is said to be passed. Because the computer is programmed by humans, it in fact constitutes a derived intelligence, and its output may be regarded as intelligently produced regardless of whether it can be confused with a human.

In SETI research, however, the challenge is to determine whether the source of a bitstring is intelligent at all. The presumption is that the source is unintelligent until proven otherwise. That’s our default. What, then, about a bitstring received from outer space could convince us otherwise? As it is, no such bitstring bearing unmistakable marks of intelligence has yet to be observed. SETI is therefore a research program that to date has zero confirmatory evidence. But that doesn’t invalidate the program. The deeper question that SETI raises—and that legitimizes it as a research program—is the counterfactual possibility that it may pan out: What about such a bitstring would convincingly implicate an intelligence if it were observed?

The Need for Small Probability

One obvious immediate requirement for any such bitstring to implicate intelligence is improbability. In other words, the event in question must be highly improbable or, equivalently, it must have small probability. What it means for an event to have small probability depends on the number of opportunities for the event to occur—or what in my book The Design Inference is called its probabilistic resources.

For instance, getting 10 heads in a row has a probability of roughly 1 in 1,000. That may seem small until one considers all the people on earth tossing coins. Factoring in all those coin-tossing opportunities shows 10 heads in a row to be not at all improbable from the vantage of human experience. But what about 100 heads in a row? Getting that many heads in a row has probability roughly 1 in 10 raised to the 30th power, or 1 in a million trillion trillion. If all the humans that have ever lived on earth did nothing with their lives but toss coins, they should never expect to see that many heads in a row. Note that if we treat heads as 1 and tails as 0, then sequences of coin tosses are equivalent to bitstrings.

So let’s imagine that a SETI researcher received a bitstring consisting of the following seven bits: 0110001. It turns out that in ASCII (American Standard Code for Information Interchange—a way of encoding keyboard characters) that this bitstring stands for the letter “a.” Now we might imagine that there was an intelligent alien who somehow learned English, knew about ASCII, and began transmitting in ASCII a long coherent English message that began with the letter “a.” Thus we might imagine the alien intended to transmit the following message: “a wonderful day has arrived on planet earth with the delivery of this message that once and for all establishes meaningful communication between our civilizations…”

Unfortunately for SETI research, this intended transmission was suddenly cut short. Only 0110001, or the letter “a” in ASCII, was transmitted. An unexpected accident prevented the rest of the message from being transmitted. And shortly after that a nuclear conflagration engulfed this alien civilization, utterly destroying it. Those precious seven bits 0110001 were therefore the product of intelligence. They were meant to denote the indefinite article.

Yet if all SETI researchers had was the bitstring 0110001, they would be in no position to conclude that this sequence of bits was intelligently generated. Why? Because the sequence is too short and therefore too probable. No SETI researcher would be justified in contacting the Wall Street Journal’s science editor on the basis of this bitstring to proclaim that aliens had mastered the indefinite article. With millions of radio channels monitored by SETI researchers, short strings like 0110001 would be bound to be observed simply as random radio noise, and not once but many times. So, one requirement for a bitstring from outer space to qualify as detectably designed is for it to be improbable in relation to any plausible chance processes that might produce it.

The Need for a Recognizable Pattern

But there’s also another requirement for such a bitstring to be detected as designed. Brute improbability is not enough. Highly improbable things happen by chance all the time. If I dump a bucket of marbles on my living room floor, their precise arrangement will be highly improbable. But if those marbles arrange themselves to spell “Welcome to the Dembski home,” we will instantly know, because of the pattern in this arrangement, that those marbles did not randomly organize themselves that way. Rather, we’ll know that an intelligence is behind that pattern of marbles, and we’ll know that even if we don’t know the precise causal story by which the intelligence acted.

This last point is important because many naturalistically inclined thinkers demand that a plausible naturalistic story must be available and fully articulated to justify any design inference. But such a requirement puts the cart before the horse. We can tell whether something is designed without knowing how it was designed or how its design was brought into physical reality. The fact is, we don’t even know the full range of naturalistic causal possibilities by which design might be implemented, so design inferences cannot be ruled in or out on purely naturalistic grounds. Design detection therefore has logical priority over the precise causal factors that may account for the design. These causal factors are downstream from whether there is design at all.

Imagine, for instance, if early humans equipped only with Stone Age tools were suddenly transported to modern Dubai. In line with Arthur C. Clarke’s dictum that “any sufficiently advanced technology is indistinguishable from magic,” our Stone Age humans visiting Dubai might think they were transported to a supernatural realm of fantasy and wonders. Yet, they would be perfectly capable of recognizing the design in Dubai’s technologies.

Of consider if we encountered extraterrestrials who use highly advanced 3D printers to create novel organisms. Rightly, we would see such organisms as designed objects even if we had no clue how the underlying technology that produced these designs worked. In general, our ability to understand broad categories of causal explanation—such as chance, necessity, or design—stems from a general familiarity with these categories of causation and not from peculiarities about how in given situations causes within these categories are applied or expressed. In particular, as beings capable of design ourselves, we can appreciate design even when we cannot recreate it. The reason lost arts are lost is not because we fail to recognize their design but because we can no longer recreate them.

It seems, then, that to detect design at the receiver of the Shannon communication diagram, as in SETI research, we need a bitstring that is at once improbable and also exhibits a recognizable pattern (similar to marbles spelling out the words “Welcome to the Dembski household”). Any long bitstring will be improbable. But the overwhelming majority of them will not be detectably designed. Our challenge, therefore, is to elaborate what qualifies as a recognizable pattern that in the presence of improbability marks a bitstring as detectably designed.

Everything and anything exhibits some pattern or other. Even a completely random bitstring that matches no pattern we might regard as recognizable conforms to some pattern. Any bitstring can be described in language (e.g., “two ones, followed by three zeros, followed by one one, ...”), and any such linguistic description constitutes a pattern. It may not be a recognizable pattern capable of detecting design, but it will be a pattern nonetheless.

Consequently, we need to define the type of pattern that makes it recognizable and therefore, in the presence of improbability, enables us to detect design. An insight by the philosopher Ludwig Wittgenstein is relevant here (from Culture and Value, my translation from the German): “When a Chinese person speaks, we hear inarticulate murmuring unless we understand Chinese and recognize that what we’re hearing is language. Likewise, I often cannot recognize the humanity in humans.”

Wittgenstein’s point, when applied to design detection, is that we must share some common knowledge or understanding with the designing intelligence behind an event if we’re going to detect design in the event. If the designing intelligence is speaking Chinese and we don’t even recognize that what is being spoken is a natural language, we may regard what we are hearing as random sounds and thus be unable to detect design. Detecting design is a knowledge-based inference (not an argument from ignorance), and it depends on a commonality of knowledge between the intelligence responsible for the design and the intelligence detecting the design.

Suppose now we witness a signal at the receiver of Shannon’s communication diagram. Let’s assume that it is a long signal, so it consists of lots of bits and is therefore improbable. To detect design, the signal therefore also needs to be recognizable. But what does it mean to say that something is recognizable? The etymology of the word recognize helps answer this question. The word derives from the Latin, the prefix re-, meaning again, and the verb cognoscere, meaning to learn or know. To recognize something is to learn or know it again. When we recognize something, there’s a sense in which we’ve already seen and understood it. It’s familiar. Aspects of it reside in our memory. Consequently, an event that is detectably designed is one that triggers our recognition. That’s the lesson for us of Wittgenstein’s insight.

Design as Double Design

An important general point about design now needs to be made, namely, that anything designed by an intelligence is doubly designed. Design always has an abstract, ideational, or conceptual aspect. And it always has a concrete, tangible, or realized aspect. It denotes imagination, intention, or plan (the conceptualization) at the front end of design. And it denotes the implementation of such conceptualizations into a physically realized form, shape, or frame (the realization) at the back end of design. Simply put, design always involves a movement from thought to thing where the designed thing expresses or approximates the designing thought.

The idea of design as double design goes back to antiquity. Thus we find the Hebrew word t‑a‑v‑n‑i‑t (תבנית without vowel points) denoting the pattern according to which something is to be made, as in Exodus 25 where God reveals to Moses on Mount Sinai the pattern according to which the tabernacle is to be made. The root of this word is b‑n‑h (בנה without vowel points), which denotes the act of building. Likewise, the Hebrew root y‑ts‑r (יצר), which denotes both imagination and realized form, captures this dual aspect of design. Double design is therefore inherent in the Hebrew understanding of design: there’s the pattern and there’s what gets built according to the pattern.

Plato argued for this view of double design in the Timaeus. In that dialogue he had the Demiurge (Plato’s world architect) organize the physical world so that it conformed to patterns residing in the abstract world of ideas. Plato referred to these patterns as forms (Greek εἶδος, transliterated eidos, from which we get our English word idea). We can equally think of these patterns as designs. Other English words getting at the same reality include essence, universal, ideal, model, type, prototype, archetype, and blueprint.

Aquinas developed this idea further with his notion of exemplary causation. An exemplary cause is a pattern or model employed by an intelligence for producing a patterned effect (see Gregory Doolan’s Aquinas on the Divine Ideas as Exemplar Causes). The preeminent example of exemplary causation within Christian theology is the creation of the world according to a divine plan, with that plan consisting of ideas eternally present in the mind of God.

The distinction between heaven and earth and even between spirit and flesh in the New Testament likewise mirrors this duality of design. Consider the Lord’s Prayer as it reads “thy will be done on earth as it is in heaven.” God’s will is done perfectly in heaven, but less so on earth. The designs in heaven are perfect, but their realization on earth is less than perfect. Interestingly, Plato’s forms are often described by philosophers as residing in a “Platonic heaven.”

An apt expression of this principle of double design appears in businessman and leadership expert Stephen Covey’s The Seven Habits of Highly Effective People. There he argues that all things are designed (or created) twice, first as a mental design and second as a physical design. Design begins with an idea, the first design, and concludes with a thing, the second design. Whatever is achieved needs first to be conceived. Design, as a process, is thus bounded by conception at one end and realization at the other. For Covey, business failure, while often not becoming evident until the second design, may already be inevitable because of a misconceived first design.

Shannon’s communication diagram epitomizes this understanding of design as double design. The diagram makes plain that the communication of information involves a fundamental duality: there’s the information as it is originated and sent on its way, and then there’s the information as it is received and implemented. At the left triad of the diagram (information source, message, and transmitter), information is conceived. At the right triad of the diagram (receiver, message, destination), information is realized. What happens on the left part of the diagram is the first design; what happens on the right is the second design.

Intuitive Design Detection

In ordinary life, design detection happens intuitively, without formal considerations or technical calculations. Here is how it works in the context of the Shannon communication diagram. Because design is always double design, an intelligence at the source of the Shannon communication diagram (in our running example, an alien intelligence) conceives of a pattern based on what it has learned and knows. It then translates that pattern into a signal transmitted across the communication channel, the signal then landing at the receiver. Next, an intelligence at the receiver, witnessing the signal, draws on its prior learning and knowledge to spot a familiar pattern. The pattern thereby becomes recognizable. And provided the signal is also improbable, the signal is inferred to be designed. In this way, its design becomes detectable.

Depending on where you are in the Shannon communication diagram, the logic of design as double design works in opposite directions. At the source, an intelligence first conceptualizes design and then actualizes it. At the receiver, an intelligence first takes something that may be an actualized design and then attempts to find a conceptualized design that matches it. Thus at the source, the logic is from conceptualization to realization; at the receiver, the logic is from realization to conceptualization.

Identifying such a conceptualized design at the receiver is the crucial moment of recognition when design is detected. Note that at the source, the logic is from cause to effect: the source thinks up the design and then (causally) brings it about as a concrete reality. But at the receiver, the logic is from effect to cause: the receiver takes what might or might not be a realized design and then must come up with a recognizable pattern that makes clear that design is actually present (or, in the absence of such a pattern, remains agnostic about whether design is actually present).

Left here, the logic of design detection falls under what philosophers call inference to the best explanation (IBE). But the logic of design detection has a mathematical basis that gives it more bite than a generic inference to the best explanation. That’s because specified complexity enables us to put numbers on the degree to which the inference is confirmed. One place we get such numbers is from the improbability of the signal whose design is in question. Another is by measuring the degree to which the signal exhibits a recognizable pattern.

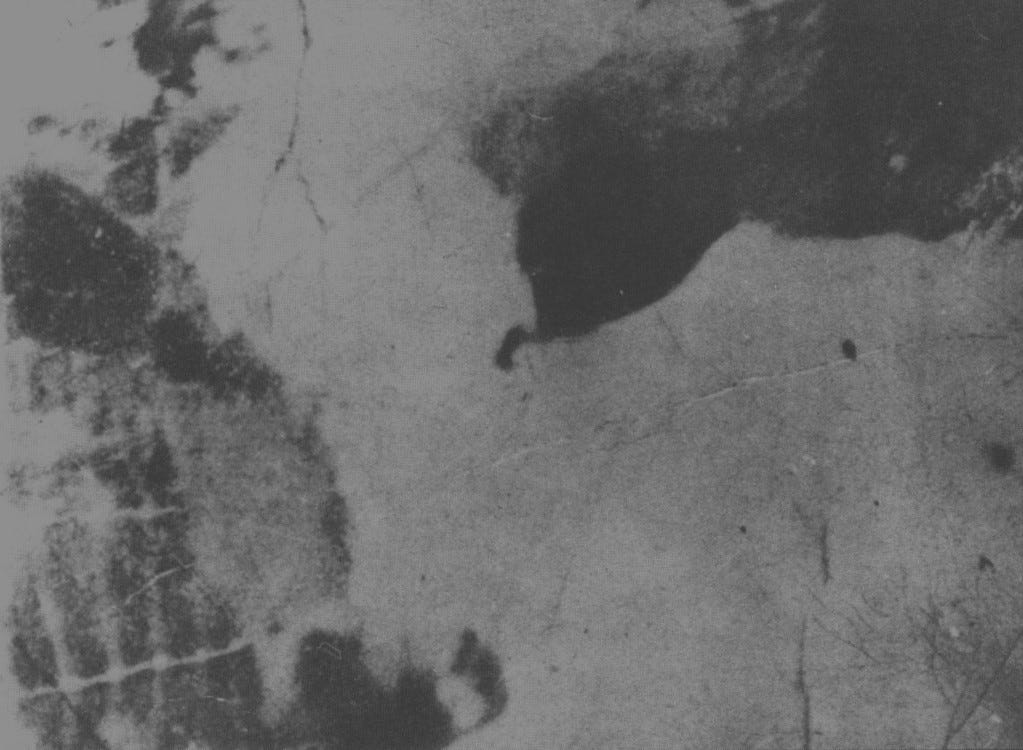
How do we put numbers on the degree of recognizability of patterns that, in the presence of improbability, lead us to detect design? We’ll discuss this shortly. But let’s be clear that in practice we detect design without attempting to measure the recognizability of patterns that lead us to detect design. Usually we just experience an aha moment of recognition. It’s as when Sherlock Holmes sees isolated pieces of evidence all suddenly converge to solve a mystery. It’s as when someone looks at what initially seems like a random inkblot but suddenly notices a familiar object that makes the design unmistakable and thus removes any possibility of these being merely random splotches of ink.

To this last point, consider the following image. If you’ve already seen this image and know what to look for or if you instantly see the familiar pattern that’s there, imagine what it would be like if you lacked this insight and saw it, at least initially, as a random inkblot. Here’s the image:

From Harold R. Booher, Origins, Icons, and Illusions

There are vastly many ways of applying ink to paper, so this image is highly improbable. If you see what’s there (woc a fo deah eht s’ti), you’ll understand it to be a recognizable pattern (if you’re still not seeing it, read the seeming nonsense words in the previous parenthesis backward). This image exemplifies how, left to our intuitions, we detect design. Nonetheless, if design detection is going to be scientifically rigorous, we’ll need to make more precise what it means for a small probability event to match a recognizable pattern.

Recognizability as Short Description Length

A rigorous theory of design detection requires that we define, in precise mathematical terms, what it is for a pattern to be recognizable. To that end, let’s return to our running SETI example. We’ve argued that improbability associated with bitstrings received from outer space is important in determining whether they are the product of intelligence. Yet the actual probability to be calculated here needs now to be clarified.

Let’s say an alien intelligence is transmitting a long English text in the ASCII coding scheme, and let’s assume noise is not a factor. What the sender sends and what the receiver receives are thus identical. Imagine then on our end we receive a long bitstring that in ASCII reads as a coherent set of English sentences. What we receive, therefore, is not word salad but sentences that connect meaningfully with each other and that together tell a meaningful story.

Let’s say the bitstring we receive is a typical paragraph of 100 words, each word requiring on average 5 letters along with a space, and each of these requiring 8 bits in ASCII (the seven usual bits along with an eighth for error correction). That’s 100 x 6 x 8 = 4,800 bits of information. Assuming a uniform probability distribution to generate these bits (let’s go with this as a first approximation—in more general technical discussions we can dispense with this assumption), that corresponds to an improbability of 1 in 2 raised to the power 4,800, or roughly 1 in 10 raised to the power 1,445. That’s a denominator with the number 1 followed by 1,445 zeros. That’s a trillion trillion trillion … where the ellipsis here requires another 117 repetitions of the word trillion.

In light of these calculations, we can now explain what the word “complexity” is doing in the term “specified complexity” and how it refers to improbability. The greater the complexity, the more improbable or, correspondingly, the smaller the probability. We see this connection clearly in this example. To achieve 4,800 bits under a uniform probability is equivalent to tossing a coin 4,800 times, treating heads as 1 and tails as 0. Getting a particular sequence of 4,800 coin tosses thus corresponds to a probability of 1 in 2 to the 4,800, or roughly 1 in 10 to the 1,445. The “complexity” in “specified complexity” is thus a measure of probability. In his theory of information, Shannon explicitly drew this connection, converting probabilities to bit lengths by applying to probabilities a logarithm to the base 2.

A probability of 1 in 10 to the 1,445 is extremely small. Moreover, the bitstring you witnessed with this small probability is clearly recognizable since the bitstring encodes a coherent English paragraph in a well-known coding scheme. And yet, that probability is not the probability we need in order to detect design. The problem is that the paragraph you received is just one of a multitude of coherent English paragraphs that you might have received, to say nothing of paragraphs coded in other ways or written in other natural languages.

Any bitstrings encoding these other paragraphs would likewise be recognizable, if not to you then to other humans. All these additional bitstrings that you might have detected as designed will thus compete against the bitstring that was recognizable and led you to detect design. A probability of 1 in 10 to the 1,445 is thus way too small for gauging whether you are in your rights to detect design. Rather, you must also factor in all the other bitstrings that might have led you to detect design. When these are factored in, the probability of witnessing not just the bitstring that you did but others comparable to it raises the probability needed to determine whether design is indeed detectable.

What typically happens, then, in detecting design is this (let’s stay with the SETI example): Operating at the source in Shannon’s communication diagram, an alien intelligence sends a given bitstring of, say, 4,800 bits across the channel. From the alien’s vantage, the probability of that sequence is 1 in 2 to the 4,800, corresponding to a complexity of 4,800 bits. But once the bitstring arrives at the receiver on earth (again, assume for simplicity no noise), it is recognized as an English message, but one among many other possible English messages. From the alien’s perspective, the message is exactly as the alien designed it and has probability 1 in 2 to the 4,800. But from the receiver’s perspective on earth, the message falls into a wider range of messages.

The receiver may thus describe the message as “an English message” or “an English message in ASCII” or “a message in a natural language.” Each of these descriptions corresponds to a range of messages where the entire range has a probability. From the receiver’s vantage on earth, what’s going to be important for detecting design is to have a description that covers a range of messages that, when taken together, still has small probability.

To see how this might backfire in negating design detection, imagine (per impossibile) that half of all ways of generating bits at random corresponded to coherent English messages in well known coding schemes. In that case, there would be no way to conclude that the message we received resulted from an alien intelligence because chance could equally well explain getting some such a message even if it is not the exact message we received.

Of course, it’s highly improbable that a random sequence of bits would form an English message in a convenient coding scheme (ASCII, Unicode, etc.). So the description “an English message” corresponds to a range of bitstrings that, taken jointly, is highly improbable. Note that sound empirical and theoretical reasons exist for estimating these probabilities to be extremely small, though doing so here would be distracting.

It’s important in this discussion to understand that by a description we don’t mean an exact identification. The description “an English message in ASCII” covers the bitstring we witnessed but also much more. It’s like rolling a six with a fair die and describing the outcome as “an even number.” This description narrows down the outcome, but it doesn’t precisely identify it. For that, we need a description that says a six was rolled. Descriptions can precisely identify, but often they set a perimeter that includes more than the observed outcome.

So what happens in the SETI example when we, at the receiver, receive this 4,800-bit bitstring? As soon as we recognize this bitstring to be a coherent English message in ASCII, we know that we’re dealing with a designed bitstring, and we consider ourselves to have successfully detected design. Moreover, at the key moment of recognition we’ll probably say to ourselves something like, “Wow, that’s an English message in ASCII.” In other words, we’ll have articulated a description such as “English message in ASCII” or “coded meaningful English text” or something like that.

But note: All these descriptions here are short AND the probability of a bitstring answering to these descriptions will be highly improbable. Now, we could as well allow ourselves longer descriptions. Imagine the text we received was coded in ASCII and comprised the first 100 words of the 262 words that make up Hamlet’s soliloquy. And now imagine our description of this bitstring to be the following, which explicitly gives the first 100 words of Hamlet’s soliloquy::

The text in ASCII that reads:
To be, or not to be, that is the question:
Whether 'tis nobler in the mind to suffer
The slings and arrows of outrageous fortune,
Or to take arms against a sea of troubles
And by opposing end them. To die—to sleep,
No more; and by a sleep to say we end
The heart-ache and the thousand natural shocks
That flesh is heir to: 'tis a consummation
Devoutly to be wish'd. To die, to sleep;
To sleep, perchance to dream—ay, there's the rub:
For in that sleep of death what dreams may come,
When we have shuffled off

Such a lengthy description would not allow us to detect design because it would have simply been read off of the bitstring we received, and we could have formed such a description for any bitstring whatsoever, including one that was randomly generated. Yes, this lengthy description precisely identifies the bitstring in question, and thus denotes a highly improbable range of bitstrings (the range here consisting of just that one bitstring). The problem is that the description is too long. If we allow ourselves long descriptions, we can describe anything, and the improbability of what we are describing no longer goes for or against its design.

Obviously, when confronted with a bitstring that encodes Hamlet’s soliloquy, what we don’t do to detect its design is repeat the entire bitstring as a description. Rather, what we do do to detect its design is come up with a short description, such as “a coherent English message” or even, if we’re familiar with Shakespeare, “Hamlet’s solioquy.”

In general, then, what is disallowed in successfully detecting design is to examine the item whose design is in question and then read off its description. That’s cheating. Rather than reading the description off the item, we want to be able to come up with it independently. That’s one reason that the descriptions needed to detect design are also called independently given patterns. The patterns are independent because we can think of them on our own without being exposed to the items whose design is in question.

All of this makes perfect sense in light of the duality of design. A sending agent conceives the design. That conceptualization may involve many complicated details, but it typically attempts to accomplish some readily stated purpose using certain well-established methods and conventions. The bitstring sent can thus be succinctly described by the receiving agent, and even though such a description may fail to precisely identify the bitstring, it will typically describe it with enough specificity that the collection of all bitstrings answering to the description will nonetheless jointly be highly improbable.

Short description length patterns along with small probability events are the twin pillars on which specified complexity rests. Together, they enable the detection of design. The importance of short description lengths to design detection can’t be overemphasized. As soon as long descriptions are allowed, they can describe anything at any level of specificity. Without a constraint on description length, small probability can’t get any traction in detecting design. And clearly, there’s a natural connection between short descriptions and recognizability—the things we are most apt to recognize are those that can be briefly described. Overly long descriptions suggest a factitiousness and artificiality at odds with recognizability.

We call the patterns with short description lengths specifications. For something to exhibit specified complexity is thus

1. for it to match a specification, which is to say for it to match a pattern with a short description length and

2. for the event answering to that pattern to have small probability.

Note that this doesn’t just mean the observed outcome has small probability. Rather, it means that the composite event of all such outcomes answering to the short-description-length pattern has small probability. In this way, short description length, or specification, and small probability, or high complexity, work together and mutually reinforce each other in detecting design.

Conclusion

In motivating specified complexity and showing why it works to detect design, I’ve omitted many details. I did in this essay sketch how Shannon information connects probability and complexity. But I omitted the connection between description length and Kolmogorov information, which is the other pillar on which the formal theory of specified complexity rests. Nor have I described how Shannon information and Kolmogorov information combine to form a unified specified complexity measure, nor how this measure exploits a deep result from information theory known as the Kraft inequality. For a first go at these details, see my article “Specified Complexity Made Simple.” For the full details, see the second edition of The Design Inference, especially chapter 6.